Interpreting geocoded data
Posted on août 10, 2014, 1:11 après-midi by Emma Tonkin
In the first post of this series, we covered the geocoding of entities in metropolitan France using INSEE data and entity data provided by expert indexers.
This process rapidly generates a large number of data points. Even though the currently published Gascon Rolls contain only a subset of the full dataset, there are already many thousands of unique entities encoded into the XML. A large subset of these appear more than once. To see what this means, it is useful to begin by describing the data model in use in the Gascon Rolls.
Data model in the Gascon Rolls
The Gascon Rolls, predictably enough, is composed of a series of rolls. These are literal rolls of material, composed of a large number of individual pieces of parchment ('membranes'), held together with a sprawling, wide-gauged zigzag stitch. The physical rolls are held by the British Archive at Kew.

This provides us with the first two components of our data model: a roll containing multiple membranes. Each membrane contains a number of entries. Each entry typically contains references to one or more entities.
So far so good: geocoding information from entities contained within an entry can therefore be used to geocode entries, membranes and rolls. Right?
Yes… and no.
Entity frequency in the Gascon Rolls
The distribution of place entities across the currently published subset of the Gascon Rolls is shown in the graphs below:
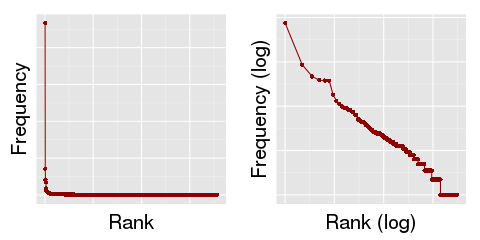
Graph: Distribution of place entities in the currently published subset of the Gascon Rolls
Practical implications for the use of geocoded data
Leaving behind the statistical technobabble, this 'long-tail' distribution (a few popular locations, many less popular locations) has practical implications for the use of this data. As we have seen in the above section, a few entities are almost ubiquitous. These entities are, therefore, not very distinctive. They do not tell you a great deal about the subject matter of a particular entry.
Compare with the frequency of words in the English language. The most common words include 'a', 'and' and 'the', but if one were building a text classification algorithm, one generally wouldn't want to classify a text according to the presence of these words, because they carry no information about the ways in which a text differs from any other. These are called 'stop-words' in search engine design, and they are typically filtered out by search engines at an early stage. They are the building blocks of a grammatically accurate English-language text, so their presence does not imply a particular type of text.
As one 'zooms out' from the entry level to the membrane, or even the roll, we begin to find ourselves with a large number of data points, always distributed in a broadly similar manner: a large number of occurrences of a small number of geographical locations, and a large number of geographical locations that appear only very seldom. A 'grammatically accurate' entry in the Gascon Rolls will tend to include a reference to Westminster in the majority of cases. Westminster is the seat of government throughout the majority of this time period; entries tend to contain what is, in effect, creation metadata referring to the seat of government. Westminster is, therefore, rather like a geographical 'stop-word', and we may not wish to consider those data points if we are looking to answer questions like, "How did the focus of the Rolls change geographically over time?" Classifying rolls, membranes or entries by geographical entity involves more than a 'word cloud' approach; we are interested not only in which locations are most common, but which are the most characteristic.
We will explore this subject further in later posts. In our next post, however, we'll discuss the visualisation of geocoded points.
References
[1] Rybski D (2013), "Auerbach’s legacy" Environment and Planning A 45(6) 1266 – 1268. Available from http://www.envplan.com/openaccess/a4678.pdf
[2] Shalizi, C (2007). So You Think You Have A Power Law - Well, Isn't That Special? Available from http://vserver1.cscs.lsa.umich.edu/~crshalizi/weblog/491.html